6. Tokens Co-occurrence and Coherence Computation¶
- Interpretability and Coherence of Topics
The one of main requirements of topic models is interpretability (i.e., do the topics contain tokens that, according to subjective human judgment, are representative of single coherent concept). Newman at al. showed the human evaluation of interpretability is well correlated with the following automated quality measure called coherence. The coherence formula for topic is defined as
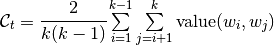 ,
,
where value is some symetric pairwise information about tokens in collection, which is provided by user according to his goals, for instance:
- positive PMI:
![value(u, v)=\left[\log\cfrac{p(u, v)}{p(u)p(v)}\right]_{+}](../../_images/math/695a2edc719faf5d420139014d78d036984c869e.png) ,
,
where p(u, v) is joint probability of tokens u and v in corpora acording to some probabilistic model. We will require joint probablities to be symetrical.
Some models of tokens co-occurrence are implemented in BigARTM, you can automatically calculate them or use your own model to provide pairwise information to calculate coherence.
- Tokens Co-occurrence Dictionary
BigARTM provides automatic gathering of co-occurrence statistics and coherence computation. Co-occurrence gathering tool is available from BigARTM Command Line Utility. Probabilities in PPMI formula can be estimated by frequencies in corpora:
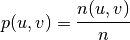 ;
;
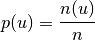 ;
;
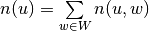 ;
;
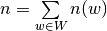 .
.
All depends of the way to calculate joint frequencies (i.e. co-occurrences). Here are types of co-occurrences available now:
- Cooc TF:
![n(u, v) = \sum\limits_{d = 1}^{|D|} \sum\limits_{i = 1}^{N_d} \sum\limits_{j = 1}^{N_d} [0 < |i - j| \leq k] [w_{di} = u] [w_{dj} = v]](../../_images/math/799f89dd3838f199e67252acda436daba0231152.png) ,
, - Cooc DF:
![n_(u, v) = \sum\limits_{d = 1}^{|D|} [\, \exists \, i, j : w_{di} = u, w_{dj} = v, 0 < |i - j| \leq k]](../../_images/math/016e67af9810d5232da2fd9999a02a5867ee3da4.png) ,
,
where k is parameter of window width which can be specified by user, D is collection, 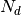 is length of document d. In brief cooc TF measures how many times the given pair occurred in the collection in a window and cooc DF measures in how many documents the given pair occurred at least once in a window of a given width.
is length of document d. In brief cooc TF measures how many times the given pair occurred in the collection in a window and cooc DF measures in how many documents the given pair occurred at least once in a window of a given width.
This document should be enough to gather co-occurrence statistics, but also you can look at launchable examples and common mistakes in bigartm-book (in russian).
- Coherence Computation
Let’s assume you have file cooc.txt with some pairwise information in Vowpal Wabbit format, which means that lines of that file look like this:
token_u token_v:cooc_uv token_w:cooc_uw
Also you should have vocabulary file in UCI format vocab.txt corresponding to cooc.txt file.
Note
If tokens has nondefault modalities in collection, you should specify their modalities in vocab.txt (in cooc.txt they’re added automatically).
To upload co-occurrence data into BigARTM you should use artm.Dictionary object and method gather:
cooc_dict = artm.Dictionary()
cooc_dict.gather(
data_path='batches_folder',
cooc_file_path='cooc.txt',
vocab_file_path='vocab.txt',
symmetric_cooc_values=True)
Where
data_pathis path to folder with your collection in internal BigARTM format (batches);cooc_file_pathis path to file with co-occurrences of tokens;vocab_file_pathis path to vocabulary file corresponding to cooc.txt;symmetric_cooc_valuesis Boolean argument.Falsemeans that co-occurrence information is not symmetric by order of tokens, i.e. value(w1, w2) and value(w2, w1) can be different.
So, now you can create coherence computation score:
coherence_score = artm.TopTokensScore(
name='TopTokensCoherenceScore',
class_id='@default_class',
num_tokens=10,
topic_names=[u'topic_0',u'topic_1'],
dictionary=cooc_dict)
Arguments:
nameis name of score;class_idis name of modality, which contains tokens with co-occurrence information;num_tokensis numberkof used top tokens for topic coherence computation;topic_namesis list of topic names for coherence computation;dictionaryis artm.Dictionary with co-occurrence statistic.
To add coherence_score to the model use next line:
model_artm.scores.add(coherence_score)
To access to results of coherence computation use, for example:
model.score_tracker['TopTokensCoherenceScore'].average_coherence
General explanations and details about scores usage can be found here: 3. Regularizers and Scores Usage.